
function [y1. yN] = myfun(x1. xM) declares a function named myfun that accepts inputs x1. xM and returns outputs y1. yN . This declaration statement must be the first executable line of the function. Valid function names begin with an alphabetic character, and can contain letters, numbers, or underscores.
You can save your function:
Files can include multiple local functions or nested functions. For readability, use the end keyword to indicate the end of each function in a file. The end keyword is required when:
Define a function in a file named calculateAverage.m that accepts an input vector, calculates the average of the values, and returns a single result.
function ave = calculateAverage(x) ave = sum(x(:))/numel(x); end
Call the function from the command line.
z = 1:99; ave = calculateAverage(z)
ave = 50
Define a function in a file named stat.m that returns the mean and standard deviation of an input vector.
function [m,s] = stat(x) n = length(x); m = sum(x)/n; s = sqrt(sum((x-m).^2/n)); end
Call the function from the command line.
values = [12.7, 45.4, 98.9, 26.6, 53.1]; [ave,stdev] = stat(values)
ave = 47.3400
stdev = 29.4124
Define a function in a file named plotData.m that plots inputs using custom parameters.
function plotData(Xdata,Ydata) plot(Xdata,Ydata,Color="black",LineStyle="-.") end
Call the function from the command line.
Xdata = 1:100; Ydata = sin(pi/20*Xdata); plotData(Xdata,Ydata)

Define a script in a file named integrationScript.m that computes the value of the integrand at 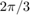 and computes the area under the curve from 0 to
and computes the area under the curve from 0 to  . Include a local function that defines the integrand,
. Include a local function that defines the integrand, 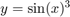 .
.
% Compute the value of the integrand at 2*pi/3. x = 2*pi/3; y = myIntegrand(x) % Compute the area under the curve from 0 to pi. xmin = 0; xmax = pi; f = @myIntegrand; a = integral(f,xmin,xmax) function y = myIntegrand(x) y = sin(x).^3; end
y = 0.6495 a = 1.3333